一、双人填数游戏# 玩家 A 和玩家 B 玩一个填数游戏。对于减式 □ □ □ □ − □ □ □ □ \square\square\square\square-\square\square\square\square □□□□ − □□□□ □ \square □ 0 ∼ 9 0\sim9 0 ∼ 9 □ \square □ s s s
1. □ − □ \square-\square □ − □ # 假设 A 举出 x x x
若 B 把 x x x x − □ x-\square x − □ 0 0 0 x x x 若 B 把 x x x □ − x \square-x □ − x 9 9 9 9 − x 9-x 9 − x 因为 B 希望最小化计算结果,因此,当 x ≤ 9 − x x\le9-x x ≤ 9 − x x ≤ 4 x\le4 x ≤ 4 x x x x x x s = min { x , 9 − x } s=\min\{x,9-x\} s = min { x , 9 − x }
回到 A 的视角,既然不管 A 出什么数,结果都是 min { x , 9 − x } \min\{x,9-x\} min { x , 9 − x } x = 4 , 5 x=4,5 x = 4 , 5 s s s 4 4 4
小结 :对于一位数的情形,A 的最优策略是出 4 4 4 5 5 5 4 4 4 s = 4 s=4 s = 4
2. □ □ − □ □ \color{red}\square\color{green}\square\color{black}-\color{red}\square\color{green}\square □ □ − □ □ # 对于 □ □ − □ □ \color{red}\square\color{green}\square\color{black}-\color{red}\square\color{green}\square □ □ − □ □ □ − □ \square-\square □ − □ □ \color{red}\square □ □ \color{green}\square □ 10 10 10 1 1 1 4 4 4 5 5 5
3. 一般情形# 对于 □ □ □ □ − □ □ □ □ \color{red}\square\color{green}\square\color{green}\square\color{green}\square\color{black}-\color{red}\square\color{green}\square\square\color{green}\square\color{green} □ □□□ − □ □□□ 4 4 4 5 5 5 □ \color{red}\square □ 0 0 0 9 9 9 □ \color{green}\square □ 1 1 1 s = 4000 s=4000 s = 4000
二、最长的接近路径# 一只蚂蚁要从起点 A 前往终点 B,AB 距离为 1 1 1
1. 蚂蚁只能恰好走 $10000$ 步,且每一步都只能走直线段; 2. 蚂蚁和终点 B 之间的距离必须严格递减。 问蚂蚁从起点走到终点,最长的路径长度是多少? 考虑只走 1 1 1 步的情形 。此时必须直接前往终点,最长路径长度是 1 1 1
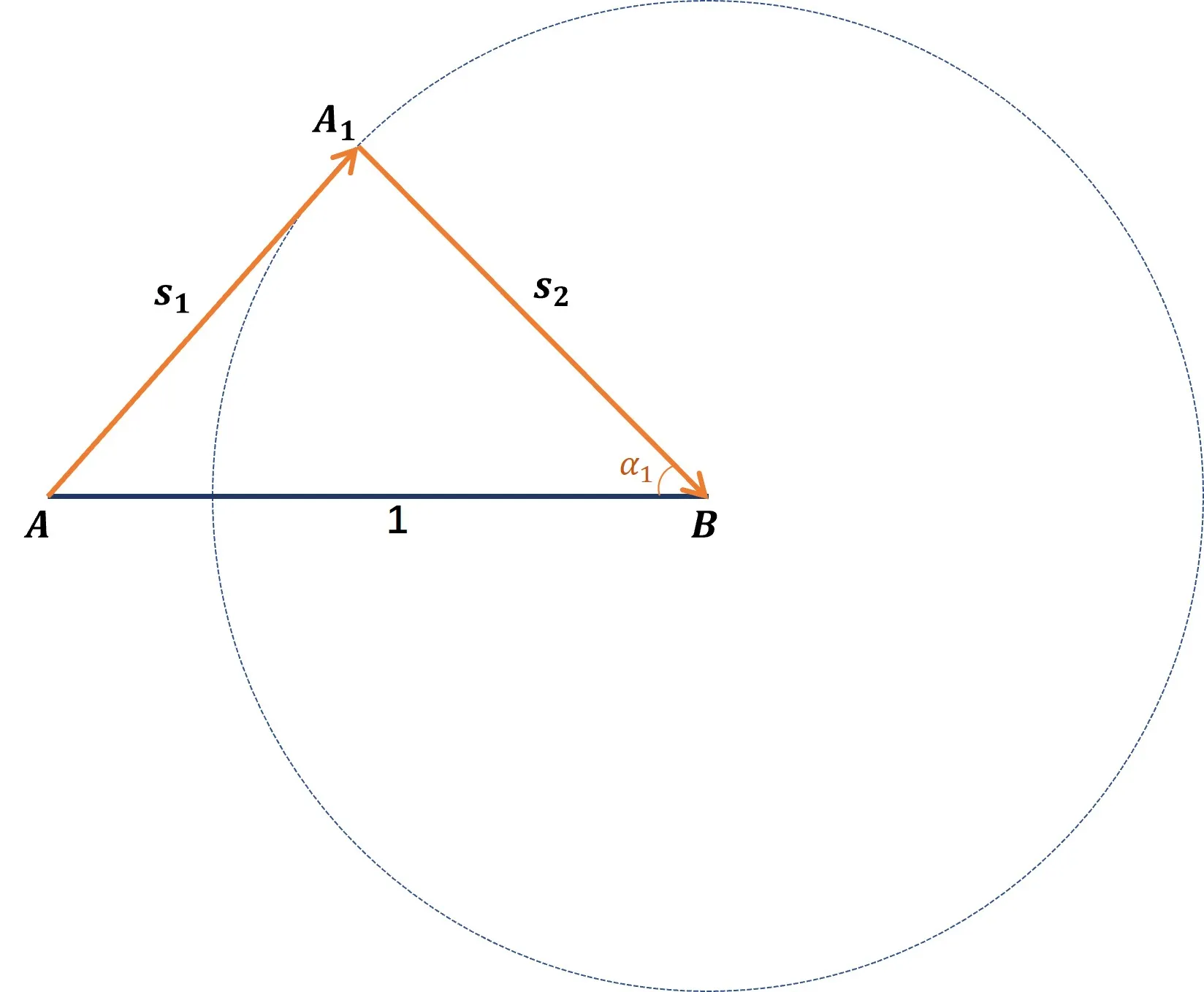
考虑走 2 2 2 步的情形 。假设蚂蚁途径点为 B B B A A 1 ⊥ A 1 B AA_1\perp A_1B A A 1 ⊥ A 1 B B B B A 1 B A_1B A 1 B
此时路径长度为
s = s 1 + s 2 = sin α 1 + cos α 1 = 2 sin ( α 1 + π 4 ) s=s_1+s_2=\sin\alpha_1+\cos\alpha_1=\sqrt2\sin\left(\alpha_1+\frac\pi4\right) s = s 1 + s 2 = sin α 1 + cos α 1 = 2 sin ( α 1 + 4 π ) 当 α = π / 4 \alpha=\pi/4 α = π /4 s s s 2 \sqrt2 2
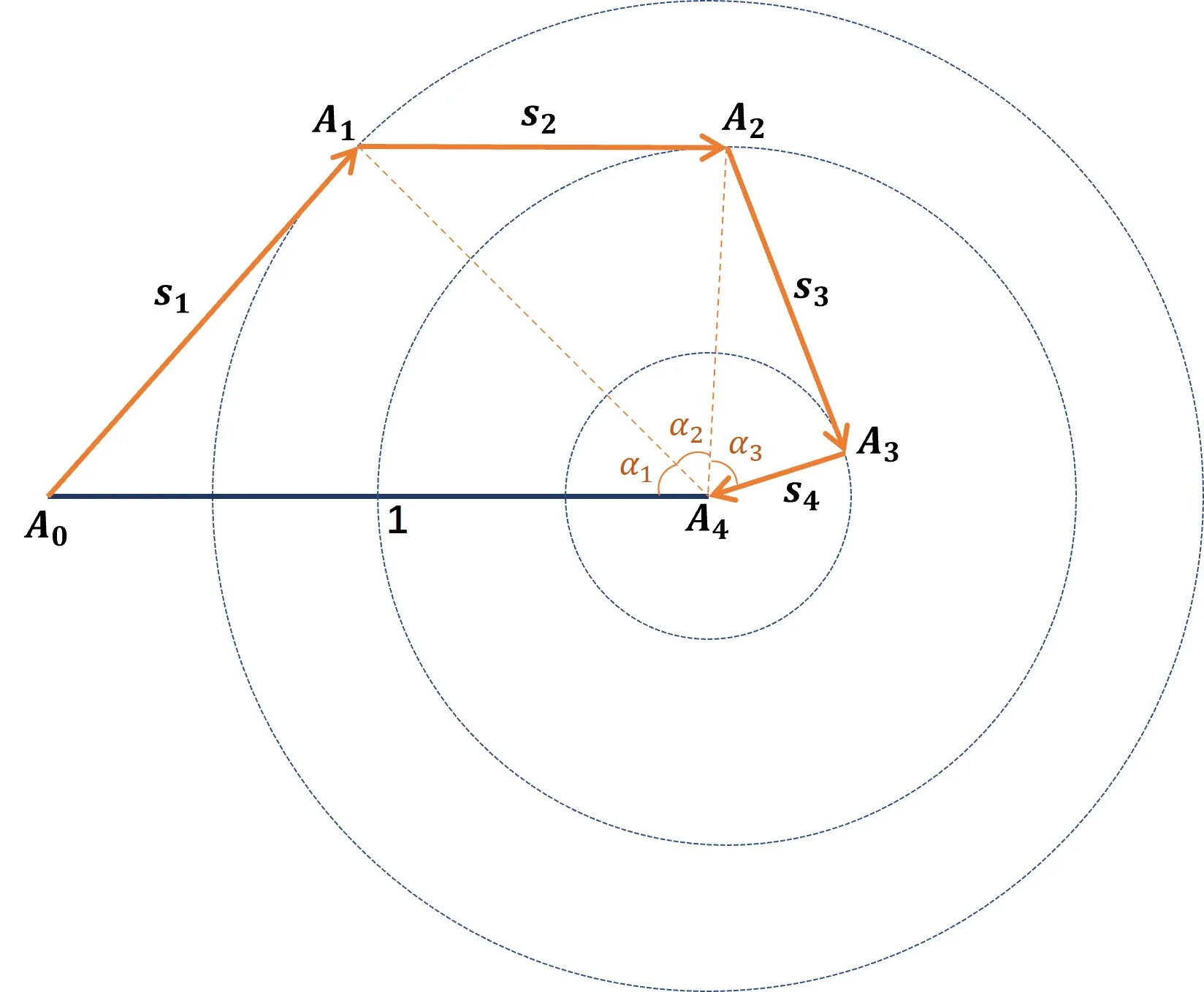
考虑走 4 4 4 步的情形 。假设蚂蚁途径各点分别为 A 0 , A 1 , ⋯ , A n A_0,A_1,\cdots,A_n A 0 , A 1 , ⋯ , A n A i A i + 1 ⊥ A i + 1 A i + 2 , 0 ≤ i ≤ n − 2 A_iA_{i+1}\perp A_{i+1}A_{i+2},\ 0\le i\le n-2 A i A i + 1 ⊥ A i + 1 A i + 2 , 0 ≤ i ≤ n − 2 n = 4 n=4 n = 4
此时路径长度为
s = ∑ i = 1 n s i = sin α 1 + cos α 1 sin α 2 + cos α 1 cos α 2 sin α 3 + cos α 1 cos α 2 cos α 3 = sin α 1 + cos α 1 sin α 2 + cos α 1 cos α 2 ( sin α 3 + cos α 3 ) ≤ sin α 1 + cos α 1 sin α 2 + 2 cos α 1 cos α 2 = sin α 1 + cos α 1 ( sin α 2 + 2 cos α 2 ) ≤ sin α 1 + 3 cos α 1 ≤ 4 . \begin{align*} s&=\sum_{i=1}^ns_i\\ &=\sin\alpha_1+\cos\alpha_1\sin\alpha_2+\cos\alpha_1\cos\alpha_2\sin\alpha_3+\cos\alpha_1\cos\alpha_2\cos\alpha_3\\ &=\sin\alpha_1+\cos\alpha_1\sin\alpha_2+\cos\alpha_1\cos\alpha_2(\sin\alpha_3+\cos\alpha_3)\\ &\le\sin\alpha_1+\cos\alpha_1\sin\alpha_2+\sqrt2\cos\alpha_1\cos\alpha_2\\ &=\sin\alpha_1+\cos\alpha_1(\sin\alpha_2+\sqrt2\cos\alpha_2)\\ &\le\sin\alpha_1+\sqrt3\cos\alpha_1\\ &\le\sqrt4. \end{align*} s = i = 1 ∑ n s i = sin α 1 + cos α 1 sin α 2 + cos α 1 cos α 2 sin α 3 + cos α 1 cos α 2 cos α 3 = sin α 1 + cos α 1 sin α 2 + cos α 1 cos α 2 ( sin α 3 + cos α 3 ) ≤ sin α 1 + cos α 1 sin α 2 + 2 cos α 1 cos α 2 = sin α 1 + cos α 1 ( sin α 2 + 2 cos α 2 ) ≤ sin α 1 + 3 cos α 1 ≤ 4 . 用数学归纳法可证明 n n n n \sqrt n n n = 10000 n=10000 n = 10000 100 100 100